nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
ISFET (Ion-Selective Field Effect Transistor): Si-SiO2 electrolyte sensor
Author:
Stefan Birner
If you want to obtain the input file that is used within this tutorial, please
submit a support ticket.
-> 1DSi_SiO2_electrolyte_sensor.in
-
Loop over pH values from pH = 0 to pH = 14.
-> 1DSi_SiO2_electrolyte_sensor_pH64.in -
This tutorial is based on the diploma thesis of Michael Bayer, TU Munich
(2004).
Acknowledgement: The author - Stefan Birner - would like to thank
Christian Uhl and Michael Bayer for helping to include the electrolyte features into nextnano³.
Si-SiO2 electrolyte sensor
Here, we predict the sensitivity of electrolyte
gate Si-SiO2 sensors to pH values of the electrolyte solution that
covers the semiconductor structure.
The charge density due to chemical reactions at the oxidic
semiconductor-electrolyte interface is described within the site-binding model ($interface-states).
We calculate the spatial charge and potential distribution both in the
semiconductor and the electrolyte (Poisson-Boltzmann equation)
self-consistently.
The Si-SiO2 sensor that is exposed to an electrolyte solution has the
following schematic layout:

Fig. 1: Si-SiO2 sensor with electrolyte gate.
We simulate the structure along the z direction
so that the structure is effectively
one-dimensional, i.e. laterally homogeneous.
The heterostructure is assumed to be grown along the [001]
direction and is not strained.
The file
densities/interface_densitiesD.txt gives us information about the
relevant interface charge densities:
- Interface 4 (1544 nm): Interface charge sigmaadsorbed that
results from the site-binding model that describes chemical reactions at the
oxidic semiconductor-electrolyte interface. More details:
$interface-states
$interface-states
state-number =
1
! between SiO2 / Electrolyte at 1544 nm
state-type
= electrolyte !
sigma_adsorbed
interface-density = 5.0d14
! [cm^-2] - total
density of surface sites, i.e. surface hydroxyl groups
adsorption-constant = 0.079433d0
! K1 = adsorption constant = 1 *
10-1.1
dissociation-constant = 2.511886d-5
! K2 = dissociation constant = 1 * 10-4.6
$electrolyte
...
pH-value
= 6.4d0
!
pH = -lg(concentration) = 6.4 -> [M]=[mol/l]
The Si region (1501 nm - 1541 nm) is homogeneously p-type doped with boron
having a
concentration of 1 * 1016 cm-3.
The electrolyte region (1544 nm - 9999 nm) contains the following ions:
!---------------------------------------------------------------------------!
! The electrolyte (phosphate buffer, NaCl) contains five types of ions:
! 1) 7 mM singly charged anions (1-)
<- 10 mM phosphate buffer (PBS) H2PO4-
! 2) 3 mM doubly charged anions (2-)
<- 10 mM phosphate buffer (PBS) HPO42-
! 3) 13 mM singly charged cations (1+)
<- 10 mM phosphate buffer (PBS) Na+
! 4) 10 mM singly charged cations (Na+)
<- 10 mM NaCl
! 5) 10 mM singly charged anions (Cl-)
<- 10 mM NaCl
!---------------------------------------------------------------------------!
$electrolyte-ion-content
ion-number =
1
!
7 mM singly charged anions
ion-valency =
-1d0 !
1-
ion-concentration = 7d-3
! Input in units of: [M] = [mol/l] = 1d-3 [mol/cm³]
ion-region =
1544d0 9999d0 ! refers to region where
the electrolyte has to be applied to
ion-number =
2
!
ion-valency =
-2d0 ! 2-
ion-concentration = 3d-3
! Input in units of: [M] = [mol/l] = 1d-3 [mol/cm³]
ion-region =
1544d0 9999d0 ! refers to region where
the electrolyte has to be applied to
ion-number =
3
!
ion-valency = 1d0
! 1+
ion-concentration = 13d-3
! Input in units of: [M] = [mol/l] = 1d-3 [mol/cm³]
ion-region =
1544d0 9999d0 ! refers to region where
the electrolyte has to be applied to
ion-number =
4
!
ion-valency =
1d0 ! Na+
ion-concentration = 10d-3
! Input in units of: [M] = [mol/l] = 1d-3 [mol/cm³]
ion-region =
1544d0 9999d0 ! refers to region where
the electrolyte has to be applied to
ion-number =
5
!
ion-valency =
-1d0 !
Cl-
ion-concentration = 10d-3
! Input in units of: [M] = [mol/l] = 1d-3 [mol/cm³]
ion-region =
1544d0 9999d0 ! refers to region where
the electrolyte has to be applied to
In addition to these five types of ions, the pH value (as specified in $interface-states)
automatically determines inside the code four further types of ions, namely the
concentration of H3O+, OH- and the
corresponding anions- (conjugate base: [anion-]
= 10-pH - 10-pOH = 10-6.4 - 10-7.6 =
3.73 x 10-7)
and cations+ (conjugate acid; zero in this tutorial for pH = 6.4 because pH = 6.4
< 7). For
details, confer $electrolyte-ion-content.
We have to solve the nonlinear Poisson equation over the whole device, i.e.
including the Poisson-Boltzmann equation that governs the charge density in the
electrolyte region.
As for the boundary conditions we assume at the right boundary
(Electrolyte/Metal) a Dirichlet boundary condition where the electrostatic
potential phi is equal to UG where UG is the gate voltage
determined by an electrode in the electrolyte solution and which is constant
throughout the entire electrolyte region. In this example the applied gate
voltage is UG = 0 V, i.e. the electrostatic potential in the
Poisson-Boltzmann equation is fixed to 0 V. Note that the reference potential UG
enters the Poisson-Boltzmann equation and also the equation for the site-binding
model at the oxide/electrolyte interface. So the Dirichlet boundary condition is
phi = 0 V. This corresponds to the fact that at the right part of the
electrolyte, i.e. at 'infinity' (at 9999 nm) the ion concentration is the
'equilibrium' (default) concentration as defined in
$electrolyte-ion-content.
At the left boundary (Metal/SiO2) we use a Neumann boundary
condition with a zero potential gradient that corresponds to an electric field E
= 0 V/m.
$poisson-boundary-conditions
poisson-cluster-number = 1
region-cluster-number = 1
boundary-condition-type = Neumann
electric-field
= 0d0 ! 0 [V/m]
poisson-cluster-number = 2
region-cluster-number = 6
boundary-condition-type = Dirichlet
potential
= 0d0 ! phi = 0 [V]
<=> UG = 0 [V]
Oxide/electrolyte interface potential as a function of pH value
The Si-SiO2 heterostructure acts as a sensor via the semiconductor-electrolyte
interface potential that reflects sigmaadsorbed, the pH value and the
spatial dependence of the electrostatic potential in the solution as described
by the Poisson-Boltzmann theory.
Choosing flow-scheme = 30, several
calculations are performed while sweeping over the pH value from 0 to 14.
pH-value
= (value is overwritten internally in the program)
The file InterfacePotentialDensity_vs_pH1D.dat gives us the
information about the electrostatic potential at the oxide/electrolyte interface
for different pH values.
The surface potential is defined as the difference of the electrostatic
potential at the oxide/electrolyte interface and the reference potential UG
(Here: UG = 0 V).
 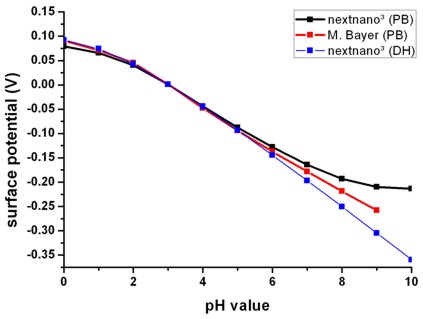
Fig. 2: Calculated oxide/electrolyte interface potential as a function of the pH
value by using the nonlinear Poisson-Boltzmann (PB) ion distribution.
For comparison the results obtained using the linear Debye-Hückel (DH) ion
distribution are also shown.
As expected, in the case of zero surface potential, the Poisson-Boltzmann and
the Debye-Hückel results are identical.
(Electrolyte: 10 mM phosphate buffer, 10 mM NaCl)
The slope (d phi / d pH) is a characteristic property of an
oxide/electrolyte interface. Note that in Fig. 2 only the slope is relevant but not the
absolute values of the potential. A linear fit between pH = 0 and pH = 9 yields
37.7 mV/pH in agreement with experiments (P. Bergveld, A. Sibbald, Analytical
and biomedical applications of ion-selective-field-effect-transistors, ed.
G. Svehla, Analytical Chemistry, Vol. XXIII, Elsevier, 1988).
Further below (Fig. 3) we see that the oxide/electrolyte interface charge density
saturates at high pH values (pH = [10,...,14]). This also means that this charge
density is then (almost) unaffected by the
oxide/electrolyte interface potential. Thus this quantity is then determined
purely by the Poisson-Boltzmann ion distribution in the electrolyte, i.e. by the
concentration of OH- (and corresponding cations+)
that are the most present ion species at high pH values.
Oxide/electrolyte interface charge density sigmaadsorbed as a
function of pH value
From the file InterfacePotentialDensity_vs_pH1D.dat we also obtain
information about the oxide/electrolyte interface sheet charge density sigmaadsorbed
(as a function of pH value) that is determined by the amphoteric reactions at
the oxide surface.
We plot in Fig. 3 the oxide/electrolyte interface
charge density sigmaadsorbed:


Fig. 3: Calculated variation of the
oxide/electrolyte interface charge density sigmaadsorbed of the
amphoteric oxide surface with the pH value of the electrolyte solution by using
the nonlinear Poisson-Boltzmann (PB) ion distribution.
Note that there is a range of pH values where the net surface charge density is
close to zero.
The calculated point of zero charge for the SiO2 surface is reached for pH =
2.2.
For comparison the results obtained using the linear Debye-Hückel (DH) ion
distribution are also shown.
At high pH values the interface charge density
saturates at the nominal density of surface sites because at the
oxide/electrolyte interface all surface sites adsorbed the hydrogen ions from
the electrolyte solution.
interface-density = 5.0d14 ! [cm^-2]
=> sigmaadsorbed = 500 * 1012 [e/cm2]
Electrostatic potential for electrolyte gate voltage UG = 0
Here we plot the electrostatic potential for a pH value of 6.4.
UG = 0 V,
i.e. we apply a zero gate voltage to the electrolyte. Note that UG is
both the Dirichlet boundary condition for the electrostatic potential at the
right contact as well as the reference potential that enters into the
Poisson-Boltzmann equation (i.e. into the exponential term of the ion charge
density).
UG is constant throughout the entire electrolyte region.
UG = 0 V:
poisson-cluster-number = 2
region-cluster-number = 6
boundary-condition-type = Dirichlet
potential
= 0d0 ! phi = 0 [V]
<=> UG = 0 [V]
Fig. 4: Spatial electrostatic potential distribution for pH = 6.4 in the
electrolyte by using the nonlinear Poisson-Boltzmann (PB) ion distribution.
For comparison the results obtained using the linear Debye-Hückel (DH) ion
distribution are also shown.
(Electrolyte: 10 mM phosphate buffer, 10 mM NaCl, UG = 0 V) |