|
| |
interface-states
To specify additional charges at material interfaces, one has to specify
- material interfaces
- interface state properties.
See also documentation under keyword
$material-interfaces.
!-------------------------------------------------------------!
$interface-states
optional !
state-number
integer
required !
state-type
character required !
fixed-charge, trap, electrolyte,
k.p
interface-density
double
required !
number-of-energy-levels
integer optional ! for trap
energy-levels-relative
double_array
optional ! for trap
degeneracy-of-energy-levels
integer_array
optional ! for trap
transition-times-cb-to-levels
double_array
optional ! for trap
transition-times-levels-to-vb
double_array
optional ! for trap
!
number-of-parameters
integer optional !
parameters
double_array optional !
adsorption-constant
double
optional ! for
electrolyte
dissociation-constant
double
optional ! for
electrolyte
!
pressure
double optional !
for gas
surface-phonon-frequencies double_array optional ! for gas (1st = weakly, 2nd
= strongly chemisorbed surface state)
accomodation-coefficients double_array optional ! gas (1st = weakly, 2nd
= strongly chemisorbed surface state)
energy-levels-chemisorbed-states double_array
optional ! gas (1st = weakly, 2nd
= strongly chemisorbed surface state)
free-molecule-energy
double optional !
gas
molecule-mass
double optional ! for gas
!
$end_interface-states optional
!
!-------------------------------------------------------------!
Syntax
state-number =
1
=
2
=
integer
Refers to state-numbers specified in
$material-interfaces.
state-type =
fixed-charge
=
trap
! The trap model is not fully tested yet. We don't have any tutorials for
it.
=
electrolyte
= gas
fixed-charge
interface-density =
-2.2d13 ! -2.2 x 1013
[|e|/cm2]
interface density of
fixed-charge
in units of [e/cm2]
trap
interface-density
= 1.0d15 ! 1.0 x 1015
[1/cm2]
[1/cm2]
number-of-energy-levels =
1
number of energy levels of this impurity
energy-levels-relative =
0.3d0 !
in units of [eV]
(can be an array of energy levels)
energy levels in [eV] relative to 'nearest'
band edge (n-type -> conduction band, else valence band)
degeneracy-of-energy-levels =
2 !
for donors
= 4 !
!
can be an array of degeneracies (one for each energy level)
transition-times-cb-to-levels =
! can be an array of transition times
trap: times from conduction band to discrete
levels
transition-times-levels-to-vb =
!
trap: times from discrete levels to valence
bands
Not included yet:
- relevant_bandedgeV = 1: Ionization energy relative to band edge
of left octant
- relevant_bandedgeV = 2: Ionization energy relative to band edge
of right octant
electrolyte
Definition of electrolyte: An aqueous solution containing dissolved
ions that result from the dissociation of salts.
The surface ionization that occurs at the oxide/electrolyte interface yields
an interfacial sheet charge density.
(Note: The pH value is specified in the keyword
$electrolyte.)
There are two ways how the electrolyte influences the calculations:
- oxide/electrolyte interface states:
$interface-states
- Poisson-Boltzmann equation in electrolyte region:
$electrolyte
$electrolyte-ion-content
!--------------------------------------------------------------------!
! Ga(x)O(y) behaves similarly to Al2O3 surface: 8.0d14 = Al2O3 value !
!--------------------------------------------------------------------!
! Amphoteric surface
!--------------------------------------------------------------------!
! S: oxide molecular site with a bonded hydroxyl group OH
!
! Two surface reactions:
! SOH_2^+ <=> SOH + H^+ : dissociation constant K_1 =
adsorption-constant
! SOH <=> SO^- + H^+ : dissociation constant K_2
= dissociation-constant
!
! SOH : neutral
! SOH_2^+: positive
! SO^- : negative
!
! total density of surface sites = total number of surface sites per unit area
= n_s
! n_s = nu_'SOH' + nu_'SOH_2^+' + nu_'SO^-'
!--------------------------------------------------------------------!
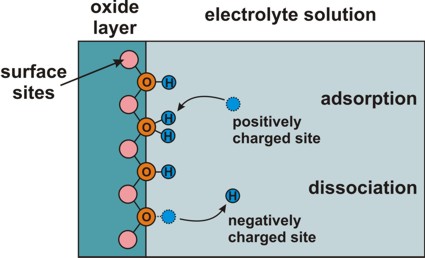
Electrolyte: Site-binding model (interface charges)
=> semiconductor/electrolyte or oxide/electrolyte interface
=> Amphoteric behavior of surface: Adsorption or
dissociation of hydrogen ions at hydroxyl (OH) groups.
Adsorption and dissociation at this interface leads to an interface charge.
interface-density
= 8.0d14 ! 8.0 x 1014
[1/cm2]
[1/cm2]
total density of surface sites, e.g. 'surface hydroxyl groups'
(S-OH)
adsorption-constant =
1.0d-8 ! K1 = adsorption
constant
dissociation-constant =
1.0d-6
! K2 = dissociation constant
These refer to the chemical reactions at the surface of the
semiconductor (or oxide) that are due to the presence of the electrolyte.
These constants
are material parameters of the semiconductor (or oxide).
In units of [-].
$electrolyte
$electrolyte-ion-content
The following figure shows the relation of the oxide/electrolyte interface
charge density sigmaadsorbed divided by the maximum possible
oxide/electrolyte interface charge density e Ns for different pH
values. Here, the electrostatic potential is taken to be fixed at phi = 0 V. The
model used here applies to amphoteric surfaces. For details confer Fig. 2.2.3
and the related description in the diploma
thesis of Michael Bayer, TU Munich (2004).

The figure shows the results for two different combinations of absorption and
dissociation constants.
adsorption-constant = 1d-6
! K1 = adsorption
constant
dissociation-constant = 1d-8 ! K2 = dissociation constant
adsorption-constant = 1d-3
! K1 = adsorption
constant
dissociation-constant = 1d-9
! K2 = dissociation constant
The following figure shows the relation of the oxide/electrolyte interface
charge density sigmaadsorbed divided by the maximum possible
oxide/electrolyte interface charge density e Ns for different
oxide/electrolyte interface potential
values. Here, the pH value is taken to be fixed at pH = 8. The
model used here applies to amphoteric surfaces. For details confer Fig. 2.2.4
and the related description in the diploma
thesis of Michael Bayer, TU Munich (2004).

To create this figure, we applied flow-scheme =
31.
- k.p interface Hamiltonian
!---------------------------------------------------------------------------!
$material-interfaces
interface-number
= 1
apply-between-material-numbers = 1 2
state-numbers
= 1 ! refers to $interface-states
state-number = 1
interface-number
= 2
apply-between-material-numbers = 2 3
state-numbers
= 2 ! refers to $interface-states
state-number = 1
$end_material-interfaces
!---------------------------------------------------------------------------!
!++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
!
pi_i D_S D_X D_Z alpha
beta1
!
! ## ==> a) Switch on k.p interface Hamiltonian
%InterfaceParameters_InAs_GaSb = +1.0 -1.70
1.17 -1.17 0.2 0.2
! [eV Angstrom] / [Angstrom] [Livneh2014]
%InterfaceParameters_GaSb_InAs = -1.0 -1.70
1.17 -1.17 0.2 0.2 ! [eV
Angstrom] / [Angstrom] [Livneh2014]
!
! ## ==> b) Switch off k.p interface Hamiltonian
! %InterfaceParameters_InAs_GaSb = 0.0
0.0 0.0 0.0 0.0 0.0
! [eV Angstrom] / [Angstrom]
! %InterfaceParameters_GaSb_InAs = 0.0
0.0 0.0 0.0 0.0 0.0
! [eV Angstrom] / [Angstrom]
!++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
!---------------------------------------------------------------------------!
! Add k.p interface Hamiltonian, see eq. (2) in
! [Livneh2012] Y. Livneh et al., Physical Review B 86, 235311 (2012).
! [Livneh2014] Y. Livneh et al., Physical Review B 90, 039903(E) (2014).
! pi_i = +1 ( normal interface, i.e. GaSb on InAs interface) or
! pi_i = -1 (inverted interface, i.e. InAs on GaSb)
!---------------------------------------------------------------------------!
$interface-states
state-number =
1
! InAs/GaSb: pi_i = +1
state-type =
k.p
interface-density = 0.0
!
number-of-parameters = 6
! pi_i D_S D_X D_Z alpha
beta
!parameters =
+1.0 -1.70 1.17 -1.17 0.2
0.2
! [eV Angstrom] / [Angstrom] [Livneh2014]
!parameters =
0.0 0.0 0.0 0.0
0.0 0.0
! [eV Angstrom] / [Angstrom] (switched off)
parameters = %InterfaceParameters_InAs_GaSb
!
state-number =
2
! GaSb/InSb: pi_i = -1
state-type =
k.p
interface-density = 0.0
!
number-of-parameters = 6
! pi_i D_S D_X D_Z alpha
beta
!parameters =
-1.0 -1.70 1.17 -1.17 0.2
0.2
! [eV Angstrom] / [Angstrom] [Livneh2014]
!parameters =
0.0 0.0 0.0 0.0
0.0 0.0
! [eV Angstrom] / [Angstrom] (switched off)
parameters = %InterfaceParameters_GaSb_InAs
$end_interface-states !
!---------------------------------------------------------------------------!
! Additional comment:
! If %DebugLevel >= 3, information on k.p interface
parameters is written to .log file.
! If %DebugLevel >= 200, the k.p Hamiltonian matrix
is written out into the debug/ folder.
! Note: For schroedinger-kp-discretization =
box-integration the imaginary part of the k.p
Hamiltonian is zero at k_parallel = 0.
!
box-integration-XYZ the imaginary part of the k.p
Hamiltonian is nonzero at k_parallel = 0.
The source code looks as follows:
!------------------------------------------------------------------------
! Add interface Hamiltonian, see eq. (2) in
! [Livneh2012] Y. Livneh et al., Physical Review B 86, 235311 (2012).
! [Livneh2014] Y. Livneh et al., Physical Review B 90, 039903(E) (2014).
!
! ==> To DO: GENERATE INPUT FILE THAT REPRODUCES FIG. 4 IN [Livneh2012].
<==
!
!------------------------------------------------------------------------
IF (kp_InterfaceL) THEN
Ham_const%matM(1,1) = Ham_const%matM(1,1) + D_S
Ham_const%matM(2,2) = Ham_const%matM(2,2) + D_S
Ham_const%matM(3,3) = Ham_const%matM(3,3) + D_X
Ham_const%matM(4,4) = Ham_const%matM(4,4) + D_X
Ham_const%matM(5,5) = Ham_const%matM(5,5) + D_Z
Ham_const%matM(6,6) = Ham_const%matM(6,6) + D_X
Ham_const%matM(7,7) = Ham_const%matM(7,7) + D_X
Ham_const%matM(8,8) = Ham_const%matM(8,8) + D_Z
Ham_const%matM(3,4) = Ham_const%matM(3,4) + pi_i *
alpha
Ham_const%matM(4,3) = Ham_const%matM(4,3) + pi_i *
alpha
Ham_const%matM(6,7) = Ham_const%matM(6,7) + pi_i *
alpha
Ham_const%matM(7,6) = Ham_const%matM(7,6) + pi_i *
alpha
Ham_const%matM(1,5) = Ham_const%matM(1,5) + pi_i * beta
Ham_const%matM(5,1) = Ham_const%matM(5,1) + pi_i * beta
Ham_const%matM(2,8) = Ham_const%matM(2,8) + pi_i * beta
Ham_const%matM(8,2) = Ham_const%matM(8,2) + pi_i * beta
END IF
gas:
The gas model is based on the so-called Wolkenstein model (Volkenstein)
which is a charge transfer model (and which is an improvement with respect
to S.R. Morrison's classical "charge transfer model").
It consists of a weakly and a strongly chemisorbed surface state.
Related terms: Electroadsorptive effect, Wolkenstein isotherm
For more information on this topic, see for instance:
- Advanced Gas Sensing: The Electroadsorptive Effect and
Related Techniques
T. Doll (Ed.)
Kluwer Academic Publishers, Boston, 2003, ISBN
1-4020-7433-6
- Chemisorption effects on the thin-film conductivity
H. Geistlinger
!interface-density =
0d0
! no gas-interface model
interface-density =
1d12
! [cm-2] total density of surface
sites
!pressure =
50d0
! [Pa] 50 Pa = 50
N/m2
(low O2)
pressure =
20d3 !
[Pa]
20 kPa = 20 kN/m2 (high O2)
surface-phonon-frequencies =
1d13
1d13
! [Hz] v0, v- 1 * 1013 Hz = 1
* 1013 1/s
! (1st = weakly, 2nd = strongly chemisorbed
surface state)
! vibration frequency of the adsorbed particle (typical value: ~1013
Hz)
accomodation-coefficients =
1d0
1d0 !
[] alpha0, alpha-
! (1st = weakly, 2nd = strongly chemisorbed
surface state)
! alpha = accomodation coefficient
energy-levels-chemisorbed-states =
-3.80d0 -7.90d0 !
Ea0,
Ea- [eV]
! (1st = weakly, 2nd = strongly chemisorbed
surface state)
free-molecule-energy
= -3.60d0 !
[eV] (Comment: Is this property related to
electron affinity?)
molecule-mass
= 31.9988d0 !
[u]
!
!
! 1 [u] = 1 / NA [g] = 1 / (1000 * NA) [kg],
where NA is
Avogadro's number.
|