nextnano3 - Tutorial
next generation 3D nano device simulator
2D Tutorial
Schrödinger equation of a two-dimensional core-shell structure
Hexagonal 2DEG - Two-dimensional electron gas in a delta-doped hexagonal shaped
GaAs/AlGaAs nanowire heterostructure
Author:
Stefan Birner
==> 2DGaAs_AlGaAs_circle_nn3.in / *_nnp.in - input file for the nextnano3 and nextnano++
software
==> 2DGaAs_AlGaAs_hexagon_nn3.in
/ *_nnp.in -
==> 2DGaAs_AlGaAs_hexagon_AlloySweep.in
-
==> 2D_Hexagonal_Nanowire_2DEG_nn3.in / *_nnp.in -
These input files are included in the latest version.
Schrödinger equation of a two-dimensional core-shell structure
In this tutorial we solve the two-dimensional Schrödinger equation of a
circular and a hexagonal GaAs/Al0.33Ga0.67As core-shell
structure.
Circular core-shell structure
==> 2DGaAs_AlGaAs_circle.in
The following figure shows the probability density of the 6th
eigenstate of the circular GaAs/AlGaAs structure.
Schroedinger_1band/2Dcb001_qc001_sg001_deg001_dir_ev006.fld
Its energy level is higher than the AlGaAs barrier energy, i.e. this
state is not confined in the circular shaped GaAs quantum well.
The horizontal and vertical slices are through the center and show the square of
the probability amplitude of this eigenstate.

The GaAs core has a radius of 5 nm. (It cannot be recognized on this plot.)
The AlGaAs shell has a radius of 15 nm. It is surrounded by an infinite barrrier
which is defined by the circular quantum region of radius 15 nm (nextnano3
input file).
(Note: The nextnano++ input file cannot use a circular quantum region.
Therefore a 15 nm x 15 nm square is used in this case as the quantum region. The
circular confinement in this case comes from the "band offset" due to the
surrounding material "air".)
Hexagonal core-shell structure
==> 2DGaAs_AlGaAs_hexagon.in
The following figure shows the conduction band edge of the hexagonal
GaAs/AlGaAs structure.
The GaAs region is indicated in black, the AlGaAs region in
blue.
Horizontal and vertical slices through the center show the energy of the
conduction band edge profile.
band_structure/cb2D_001_sub001.fld
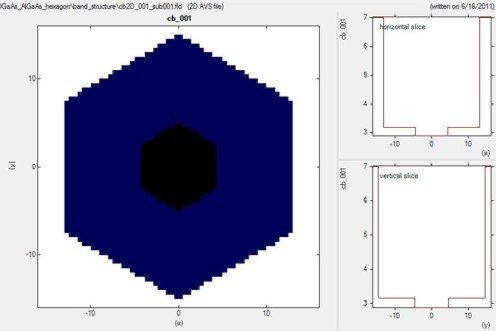
The diameter of the hexagonal shaped GaAs core is ~8.66 nm (corresponding to
an outer radius of the core of 5 nm).
The diameter of the hexagonal shaped AlGaAs shell is ~26 nm (corresponding to an
outer radius of the shell of 15 nm).
The following figure shows the probability density of the 10th
eigenstate of the circular GaAs/AlGaAs structure.
Schroedinger_1band/2Dcb001_qc001_sg001_deg001_dir_ev010.fld
Its energy level is higher than the AlGaAs barrier energy, i.e. this
state is not confined in the hexagonal shaped GaAs quantum well.
The horizontal and vertical slices are through the center and show the square of
the probability amplitude of this eigenstate.

The hexagonal GaAs core has an outer radius of 5 nm. It cannot be seen on
this plot.
The AlGaAs shell has a diameter of 26 nm. It is surrounded by an infinite
barrrier which is defined by the hexagonal shaped quantum region of diameter 26
nm (nextnano3 input file).
(Note: The nextnano++ input file cannot use a hexagonal quantum region.
Therefore a 16 nm x 16 nm square is used in this case as the quantum region. The
hexagonal confinement in this case comes from the "band offset" due to the
surrounding material "air".)
Alloy sweep
==> 2DGaAs_AlGaAs_hexagon_AlloySweep.in
(There is no nextnano++ input file
available that performs an alloy sweep as this feature is not supported in the
input file. But you can use nextnanomat's
Template feature to perform an alloy
sweep with nextnano++.)
In the following, we vary the alloy content x of the ternary AlxGa1-xAs
from 0 to 0.33 in 11 steps.
$alloy-function
material-number
= 2
function-name
= constant ! spatially constant alloy
content
xalloy
= 0.0d0 !
alloy-sweep-active
= yes !
alloy-sweep-step-size =
0.03d0 !
alloy-sweep-number-of-steps = 11
!
For x = 0, we have pure GaAs.
For x = 0.33 we have an AlGaAs/GaAs conduction band offset of 0.285 eV, and a
valence band offset of -0.168 eV.
In the latter case, the quantum confinement is stronger.
Even for x = 0 we have "quantum confinement" due to the Dirichlet boundary
conditions (corresponding to infinite barriers) at the shell surface that we use
for the Schrödinger equation.
Consequently, even for x = 0, we get an e1-h1 transition
energy from the lowest electron state (e1) to the highest heavy hole
state (h1) that is larger than the band gap as shown in the following
figure.
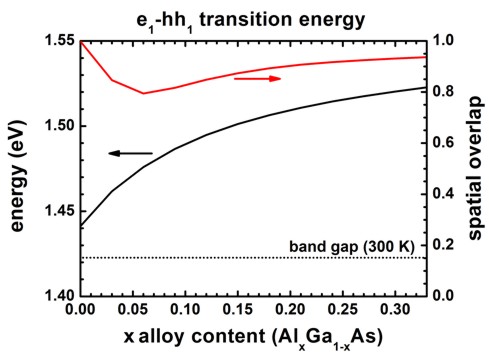
The transition energies (e1-h1), as well as the spatial
overlap intergral of the electron and hole ground state wave functions, are
contained in this file:
sweep_interband2D_qc001_vb001_sg001_cb001_sg001_deg001_dir.dat
alloy type
el-hl[eV] el[eV]
hl[eV] matrix_element
0.330000 |<psi_vb001|psi_cb001_>|^2 1.522777615
2.965889676 1.443112062 0.936344908
0.300000 |<psi_vb001|psi_cb001_>|^2 1.520316794
2.963669699 1.443352905 0.931291593
...
The spatial overlap of electron and hole wave functions is always very high.
When there is only confinement due to the shell boundary, the matrix element is
very high (99.8 %).
The matrix element must be smaller than 1 for x = 0 because the electron and
hole masses are different.
The matrix element must be even smaller (94 %) for x = 0.33 (strong confinement)
because in addition to the mass difference, the conduction and valence band
offsets are not equivalent.
The matrix element has a minimum at around x = 0.06 because in this case the
electron wave function penetrates into the barrier much stronger that the hole
wave function does.
Thus the differences in well and barrier masses (as well as band offsets) play a
high role for the spatial extension of the wave functions.
Sweep over further variables
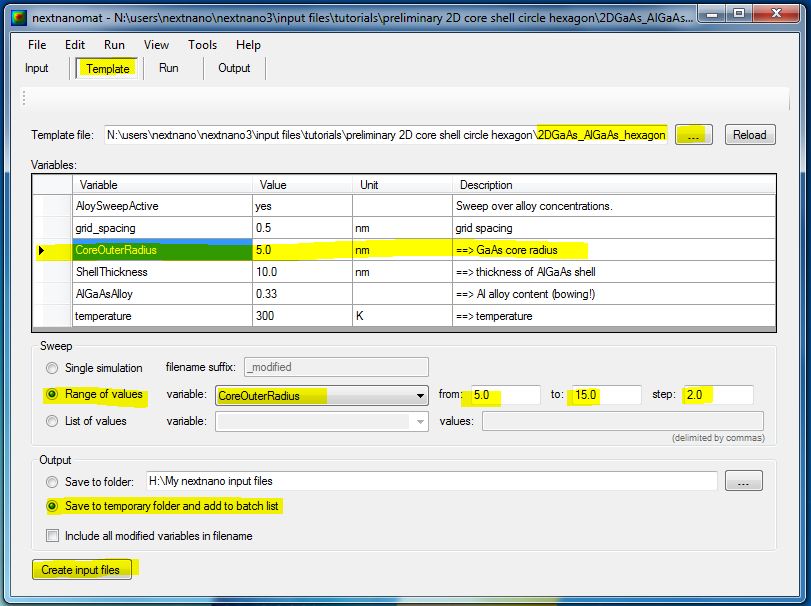
It is also possible to sweep over variables, like e.g. the outer radius of
the GaAs core ("CoreOuterRadius") using nextnanomat's
"Template" feature.
Just select "Range of values", choose the variable
to be swept over, and specify a "from" "to"
range, and the "step".
The click on "Create input files" and switch to the
"Run" pane to start your batch list.
You can define your own variables using macros.
Macros are described here.
Hexagonal 2DEG - Two-dimensional electron gas in a delta-doped hexagonal
shaped GaAs/AlGaAs nanowire heterostructure
==> 2D_Hexagonal_Nanowire_2DEG.in
The following example deals with a delta-doped GaAs/AlGaAs 2DEG
(two-dimensional electron gas) structure.
In this case, the heterostructure consists of a hexagonal GaAs/AlGaAs nanowire.
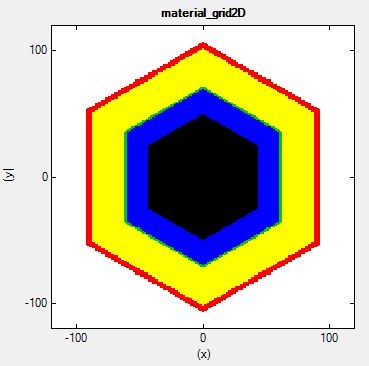
The material layers are shown here in the following figure which shows the
content of this file: material_grid2D.fld
- black: GaAs core
- blue: AlGaAs spacer
- green:
Si-doped AlGaAs
- yellow:
AlGaAs
- red: GaAs capping layer
-
white: Schottky barrier contact: The white layer itself is not
included in the calculation. It only serves as a boundary condition.
 |

Artist's view of a hexagonal nanowire.
(The artist is 4 years old. ;-) |
The self-consistently calculated conduction band edge (band_structure/cb2D_Gamma_sub001.fld)
is shown next.
The horizontal and vertical slices through the center indicate the triangular
potential well (conduction band minimum) where the 2DEG is located.

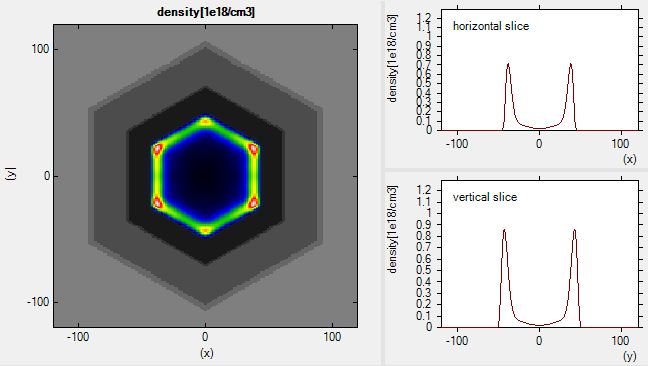
The resulting 2DEG electron density (densities/density2Del.fld)
is shown in the following figure.
At the corners, the electron density is significantly higher, thus
one-dimensional conducting channels are formed.
Although the structure itself has a hexagonal symmetry, our rectangular grid
breakes this symmetry.
Therefore the density in the upper/lower corner are different from the density
at the left/right corners.
The 2D Poisson equation and the 2D Schrödinger equation have been solved
self-consistently.
The dimension of the Schroedinger matrix is 28,625.
The CPU time for this calculation was about 18 minutes.
| 

