nextnano³ - Tutorial

1D Tutorial

Simple quantum cascade structure

-> 1DQCL_simple_nn3.in / *nnp.in - input file for the nextnano³ and nextnano++ software
 

Simple quantum cascade structure - Results

This tutorial is based on the quantum-cascade structure (Figures 12 (b) and 16 (b)) that has been presented in the following paper:

Resonant Tunneling Through Double Barriers, Perpendicular Quantum Transport Phenomena in Superlattices, and Their Device Applications
F. Capasso, K. Mohammed, A.Y. Cho
IEEE Journal of Quantum Electronics QE-22 (9), 1853 (1986)

The following picture is based on Fig. 3 of

Simulation of quantum cascade lasers - optimizing laser performance (in English)
S. Birner, T. Kubis, P. Vogl
Photonik international 2, 60 (2008)

Simulation zur Optimierung von Quantenkaskadenlasern (in German)
S. Birner, T. Kubis, P. Vogl
Photonik 1, 44 (2008)

It shows the conduction band edge profile of an Al_0.48In_0.52As/In_0.53Ga_0.47As superlattice at an electric field of -89 kV/cm.
The single-band effective-mass Schrödinger equation is solved for this band profile.
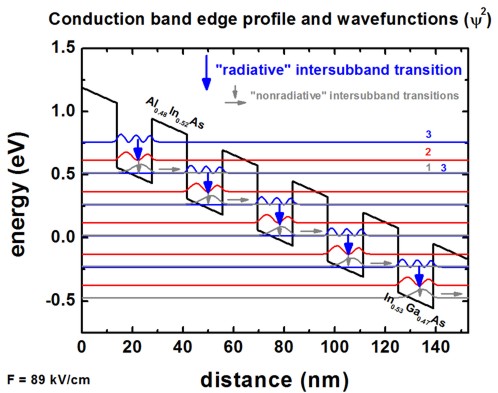
The wave functions (psi²) of this quantum cascade structure are shown.

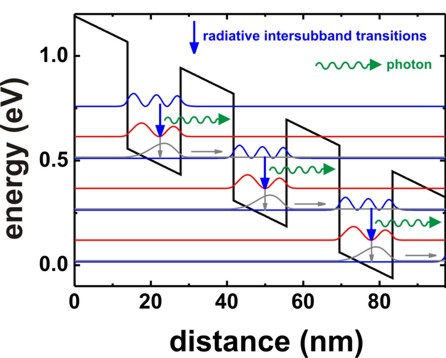
The basic idea of such a structure is to depopulate the lowest eigenstate of each quantum well efficiently by bringing it into resonance with the third eigenstate of the next quantum well (resonant tunneling).
The transition second eigenstate -> lowest eigenstate should be a nonradiative intersubband transition whereas
the transition third eigenstate -> second eigenstate should be a radiative intersubband transition, i.e. a photon is emitted.
Another important condition for a quantum cascade laser is population inversion,
i.e. the occupation of the third eigenstate must be much higher than the occupation of the second eigenstate and lowest eigenstate.

• The input file "1DQCL_simple.in" should be rather intuitive and self-explanatory.
  Documentation for each keyword and each specifier can be found here: keywords
   
• An example of a keyword ($electric-field) and a specifier (electric-field-strength) is the electric field.
  
  The electric field is set to -89 kV/cm.
  
   $electric-field
  ...
  electric-field-strength = -89d5 ! in units of [V/m] - Here: -89 kV/cm (d5 = 105, i.e. -89 * 105 [V/m])
 

Output

The output files are ASCII files and can be plotted with software like e.g. Origin.

• The conduction band edge can be found in the following file:
  
band_profile/cb_Gamma.dat
  
  1^st column:  grid points in units of [nm]
  2^nd column: Gamma conduction band edge in units of [eV]

If one plots the content of this file, one gets the following figure.
  
  
  
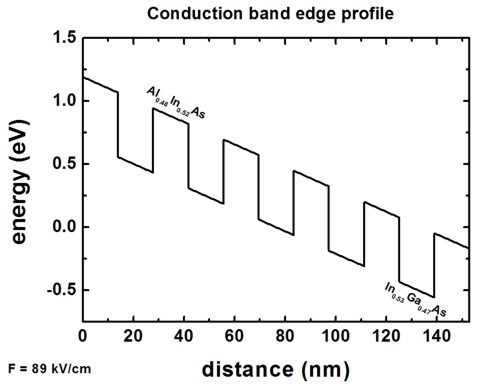
  There are six Al_0.48In_0.52As barriers and five In_0.53Ga_0.47As barriers.
  The conduction band offset is 0.51 eV.
   
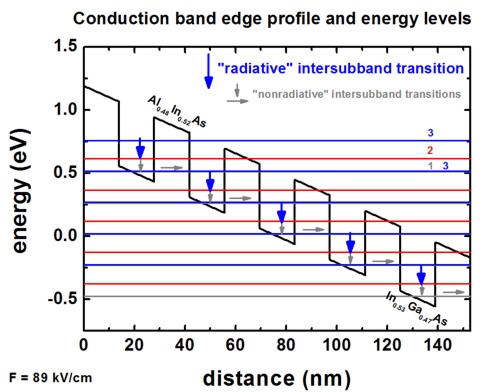
• The 40 eigenvalues that were calculated can be found in this file:
  wavefunctions/ev_cb1_sg1_deg1.dat
The units are [eV].

The eigenvalues are also contained in this file, i.e. the eigenvalues for each grid point
  wavefunctions/cb1_qc1_sg1_deg1_psi_squared_shift.dat
1^st column:       grid points in units of [nm]
  2^nd column:      1^st eigenvalue in units of [eV]
3^rd column:      2^nd eigenvalue in units of [eV]
...
41^st column:     40^th eigenvalue in units of [eV]

If one plots these columns (together with the conduction band edge) one obtains the following picture:



Note: The figure shows only the following energy levels: 1,2,3,4,5,9,10,12,16,18,20,26,27,30,37
 
• The square of the wave functions (psi²) of the 40 eigenstates can be found in this file
  wavefunctions/cb1_qc1_sg1_deg1_psi_squared_shift.dat
1^st column:       grid points in units of [nm]
  ...
42^nd column:    psi² of 1^st eigenstate
43^rd column:     psi² of 2^nd eigenstate
...
81^st column:     psi² of 40^th eigenstate

Note: In order to be able to plot the wave functions nicely into the conduction band edge profile, we shift the square of the wave function by its corresponding energy: psi²_n' = psi²_n + E_n

If one plots these columns (together with the conduction band edge) one obtains the following picture:
  


Note: The figure shows only the following wave functions: 1,2,3,4,5,9,10,12,16,18,20,26,27,30,37

The basic idea of such a structure is to depopulate the lowest eigenstate of each quantum well efficiently by bringing it into resonance with the third eigenstate of the next quantum well (resonant tunneling).
  The transition 2 -> 1 should be a nonradiative intersubband transition whereas
  the transition 3 -> 2 should be a radiative intersubband transition, i.e. a photon is emitted.
  Another important condition for a quantum cascade laser is population inversion,
  i.e. the occupation of the state 3 must be much higher than the occupation of the states 2 and 1.
   
• The conduction band masses that were used for each grid point can be found in this file:

conduction_band_masses1D.dat

1^st column:       grid points in units of [nm]
  other columns: effective mass tensor components of Gamma, L and X valleys in units of [m₀]
            m(Gamma)  m(Gamma)  m(Gamma)   ml(L)  mt(L)  mt(L)   ml(X)  mt(X)  mt(X)

These masses have been calculated from the binaries InAs, GaAs and AlAs for the relevant ternaries, including bowing parameters.
 
• Experienced users might be interested in having a look at the intersubband matrix elements:
  
  The intersubband (or intraband) matrix elements p_z and the oscillator strengths can be found in this file:
  
wavefunctions/intraband_pz1D_cb001_qc001_sg001_deg001_dir.txt

The content of this file should not be plotted! One has to open this file with a text editor.

More information and documentation on these matrix elements is available here: Intersubband matrixelements