nextnano³ - Tutorial

next generation 3D nano device simulator

1D Tutorial - Part 6

Piezoelectric fields due to strain (Quantum well)

Information on strain can also be found in the FAQ section and in the strain tutorial.

Author: Stefan Birner

If you want to obtain the input files that are used within this tutorial, please check if you can find them in the installation directory.
If you cannot find them, please submit a Support Ticket.
-> 1Dpiezo_Al0.70In0.30As_In0.53Ga0.47As_100_nn3_growth_along_z_direction.in -input file for the nextnano³ software
1Dpiezo_Al0.70In0.30As_In0.53Ga0.47As_311_nn3_growth_along_z_direction.in -input file for the nextnano³ software
1Dpiezo_Al0.70In0.30As_In0.53Ga0.47As_100_nn3.in / *_nnp.in - input file for the nextnano³ and nextnano++ software 1Dpiezo_Al0.70In0.30As_In0.53Ga0.47As_311_nn3.in / *_nnp.in -input file for the nextnano³ and nextnano++ software 1Dpiezo_Al0.33In0.67As_In0.32Ga0.68As_111_nn3.in / *_nnp.in -input file for the nextnano³ and nextnano++ software

Input files for nextnano.MSB and nextnano.NEGF software for this tutorial are also available.

Piezoelectric fields Piezoelectricity is due to the ionicity of III-V semiconductor compounds. Si and Ge have purely covalent bonds whereas the bonds of III-V compounds are partially ionic (heteropolar) because the electrons spend on average more time next to the (negatively charged) anions. Zinc-blende structures are piezoelectric materials. Off-diagonal strain tensor components (j≠k) induce a polarization given by P_i^s= 2 e₁₄ epsilon_jk (epsilon = strain tensor) where P^s is the induced polarization, e₁₄ is the piezoelectric constant and epsilon_jk is a symmetrized strain component. However, diagonal strains (epsilon_xx, epsilon_yy, epsilon_zz) do not induce a polarization (i.e. e₁₁=0). A strained layer superlattice with a [001] growth direction will induce only diagonal strains; but with any other growth direction, off-diagonal strains also occur. Thus [001]-growth axis strained-layer heterostructures will not have strain-induced polarization fields, but strained-layer heterostructures with any other growth direction will have these polarization fields. Because one of the constituent materials is in biaxial tension and the other is in biaxial compression, the polarization vector changes sign at the interface. For a [111] growth axis, P^s is parallel to the growth axis, for a [110] growth axis, P^s is in the interface plane; for a [001] growth axis, P^s vanishes. For a general growth axis, P^s has components both parallel and perpendicular to the growth axis. The resulting interface charge density is given by rho = - div P^s. `==>` Text taken from D.L. Smith, C. Mailhiot, Rev. Mod. Phys. 62 (1), 173 (1990) Thus we want to test this on a quantum well structure consisting of Ga_0.47In_0.53As (quantum well) and Al_xIn_1-xAs (barrier). We will try 3 growth directions for Al_0.70In_0.30As. [001] - no strain-induced polarization fields (E=0) [011] - polarization vector P^s lies in the interface plane [111] - polarization vector P^s is perpendicular to interface and parallel to growth direction (A superlattice grown in [111] direction has a different point group symmetry, namely C_3v, than [001] growth which is D_2d.) We will also try growth direction [111] with different alloy compositions for the barrier resulting in different piezoelectric constants for each barrier material. Al_0.63In_0.37As Al_0.33In_0.67As Ga_0.47In_0.53As/Al_0.48In_0.52As is lattice matched to InP. By proper choice of alloy composition of Al_xIn_1-xAs, one can subject this layer to either tensile or compressive strain when grown pseudomorphic on InP leading to a splitting in light hole (lh) and heavy hole (hh) bands and also changing their order. Okay, let's compare the growth directions for a Ga_0.47In_0.53As - Al_0.70In_0.30As quantum well.
along [001] direction `==> 1Dpiezo_Al0.70In0.30As_In0.53Ga0.47As_100_nn3_growth_along_z_direction.in` Splitting due to strain: The heavy hole band (vb1) is lower than the light hole band (vb2) of Al_0.70In_0.30As (barrier) due to tensile strain. Due to the [001] growth direction, no piezoelectric charges are present.
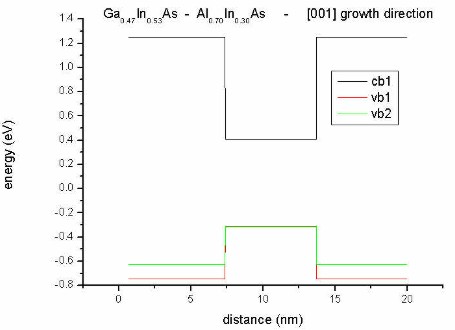	Conduction and valence bands along [001]
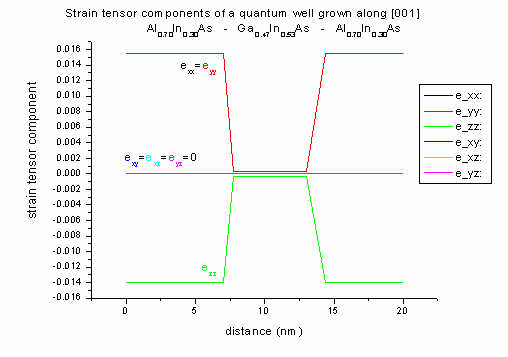	Strain along [001]
[001] growth direction: The well region is lattice matched to InP, therefore strain is zero. Only the barrier region is subject to strain. The off-diagonal strain tensor components are all zero (e_xy=e_xz=e_yz=0) as we have [001] growth direction. Al_0.70In_0.30As has a smaller lattice constant than the substrate material InP (lattice mismatch 1.55 %) leading to tensile strain. In 1D strain can be calculated analytically along [001] growth direction: (a = lattice constant, c₁₁, c₁₂ = elastic constants): Biaxial strain (in plane of interface): e_xx= e_yy = ( a_substrate - a_layer ) / a_layer = 0.0155 (1.55 % lattice mismatch) Uniaxial strain (perpendicular to interface): e_zz= - 2 (c₁₂/c₁₁)e_xx = - 0.014 For [001] growth direction, crystal and simulation system coincide. Thus the strain given in the crystal coordinate system is equal to the strain given in the simulation system.
along [011] direction changes in input file: `hkl-z-direction-zb = 0 1 1 !` Miller indices of z coordinate axis [0 0 1]`hkl-y-direction-zb = 0 1 -1 !`Miller indices of y coordinate axis [0 1 0] There's no effect due to piezoelectric charges as the polarization vector is directed along the interface (perpendicular to growth direction).
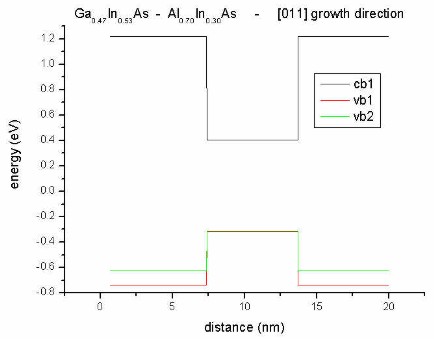	Conduction and valence bands along [011]
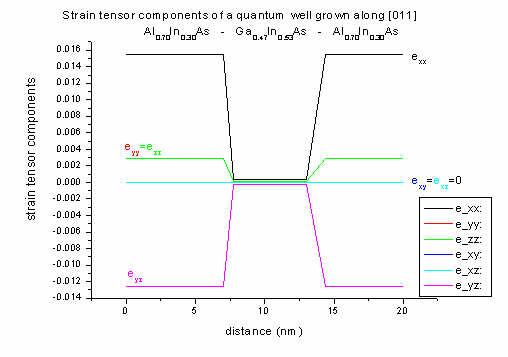	Strain along [011]
[011] growth direction: The well region is lattice matched to InP, therefore strain is zero. Only the barrier region is subject to strain. e_xxagain can be calculated analytically as above with the same result. The off-diagonal strain components that include x are zero (e_xy=e_xz=0). Due to shear strain in the (y,z) plane, e_yz is not zero. Al_0.70In_0.30As has a smaller lattice constant than the substrate material InP (lattice mismatch 1.55 %) leading to tensile strain. In 1D layered heterostructures, strain can be calculated analytically along [011] growth direction (see FAQ section). The strain tensor components can be printed out with respect to the crystal coordinate system and simulation coordinate system (see keyword`$output-strain`). For [011] growth direction, crystal and simulation system do not coincide anymore. Thus the strain given in the crystal coordinate system is not equal to the strain given in the simulation system anymore. In the simulation system all off-diagonal components of the strain tensor are zero (e_xy,sim=e_xz,sim=e_yz,sim=0) and e_yy,sim=e_zz,sim.
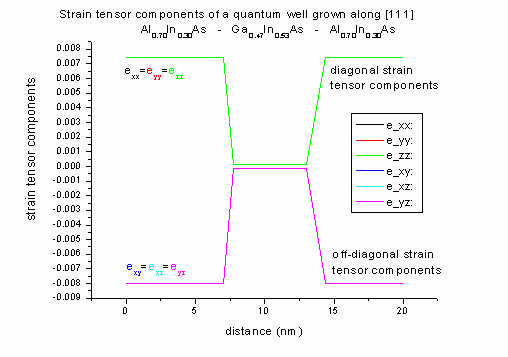
along [111] direction changes in input file: `hkl-z-direction-zb = 1 1 1 !` Miller indices of z coordinate axis [1 1 1]`hkl-y-direction-zb = 0 1 -1 !`Miller indices of y coordinate axis [0 1 -1] The polarization vector due to piezoelectric charges is directed along the [111] growth direction leading to a slope in the conduction and valence bands.
	Conduction and valence bands along [111]
	Strain along [111]
[111] growth direction: The well region is lattice matched to InP, therefore strain is zero. Only the barrier region is subject to strain. In 1D strain can be calculated analytically along [111] growth direction (see FAQ section). The off-diagonal strain components (shear strain) are all equal (e_xy=e_xz=e_yz). Al_0.70In_0.30As has a smaller lattice constant than the substrate material InP (lattice mismatch 1.55 %) leading to tensile strain. For [111] growth direction, crystal and simulation system do not coincide either. Again, the strain given in the crystal coordinate system is not equal to the strain given in the simulation system. In the simulation system all off-diagonal components of the strain tensor are again zero (e_xy,sim=e_xz,sim=e_yz,sim=0) and e_yy,sim=e_zz,sim. Note: For [321] growth direction e_yz,sim=0 but all other off-diagonal compontents are not zero anymore. In the simulation system, for any growth direction, e_yy,sim=e_zz,sim=e_xx,sim^[111]=e_xx,sim^[hkl]. For the pictures above, the strain tensor components are plotted with respect to the crystal coordinate system, not simulation coordinate system.

Discussion of piezoelectric field
For the [111] case the polarization vector is along [111]. As expected we get an electric field. For [011] the polarization vector lies in the interface (no resulting E field) and for [001] there isn't any polarization verctor.

([111] growth: If you change the piezoelectric constant e₁₄ in the `database_nn3.in` file to zero, you won't get a slope and the picture looks as for the [001] case. If you change the signs of these constants from negative to positive, the slope would be reversed. The direction depends on the sign, e.g. positive from In (cation) to As (anion) along [111].) You can also switch of piezoelectricity using the flag`piezo-constants-zero = yes`in`$numeric-control`.
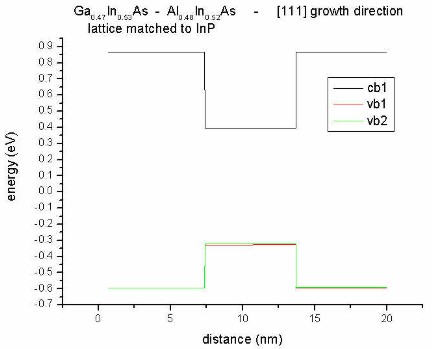
along [111] direction Again we take the [111] direction but this time we take lattice matched Ga_0.47In_0.53As and Al_0.48In_0.52As (lattice matched to InP) herby avoiding any strain. Thus we do not get any heavy hole/light hole splitting. Without strain we even don't get piezoelectric charges and thus no slope.

along [111] direction Here, we change the alloy composition of the barrier. (strain calculation: pseudomorphic on InP substrate: `homogeneous-strain`) - biaxial compression for Al_0.33In_0.67As - biaxial tension for Al_0.63In_0.37As - still no strain for the well Now the electric field resulting from piezoelectric charges changes its direction in the two cases. The heavy hole (vb1) / light hole (vb2) splitting is also different in these two cases!
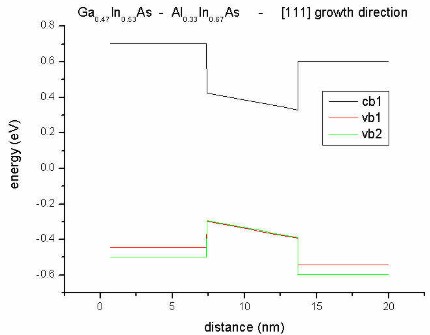	biaxial compression for Al_0.33In_0.67As
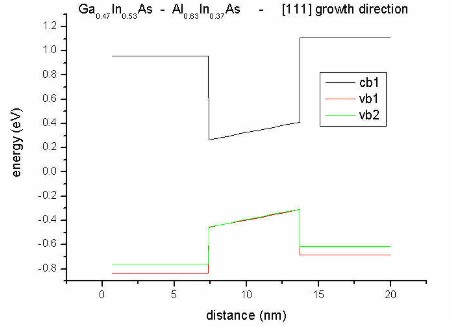	biaxial tension for: Al_0.63In_0.37As

along [111] direction Our substrate is InP. We now combine compressive (Ga_0.32In_0.68As) and tensile (Al_0.63In_0.37As) strain. Now for both materials, heavy hole (vb1) and light hole (vb2) bands split but into opposite directions.
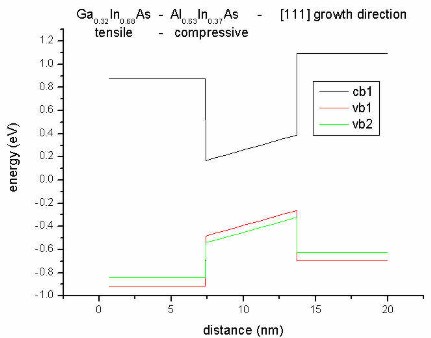	biaxial tension for: Al_0.63In_0.37As (barrier) biaxial compression for: Ga_0.32In_0.68As (well)
along [111] direction `==> 1Dpiezo_Al0.33In0.67As_In0.32Ga0.68As_111_nn3.in` Our substrate is InP. We now combine tensile (Ga_0.68In_0.32As) and compressive (Al_0.33In_0.67As) strain. Now for both materials, heavy hole (vb1) and light hole (vb2) bands split again but into opposite directions and into opposite directions compared to the previous pictures.
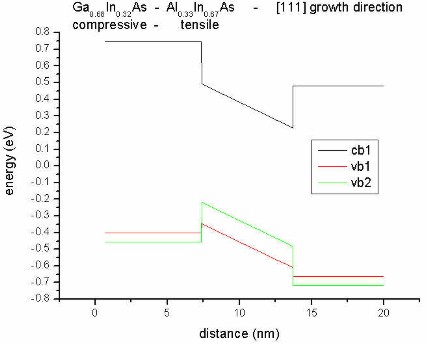	biaxial compression for: Al_0.33In_0.67As (barrier) biaxial tension for: Ga_0.68In_0.32As (well)

Step 1: Quantum well structure - Piezoelectric fields

The structure is grown pseudomorphic on an InP substrate.
We perform a one-dimensional simulation.
Just a reminder: If you need additional information about the keywords and their specifiers, you can look it up here.
The heterostructure looks like this:

! barrier well barrier ! 1 2 3 ! ! Al(x)In(1-x)As In(x)Ga(1-x)As Al(x)In(1-x)As ! 7 6 7 nm !___________________________________________________
The structure has no doping.
Output
- The band structure will be saved into the directoryband_profile/- The densities will be saved intodensities/- The strain will be saved intostrain/- The material parameters will be saved into material_parameters/
You should be able to modify the appropriate lines in the input file 1Dpiezo.inin order to reproduce the results shown above.
$domain-coordinates ... $end_domain-coordinates $alloy-function ... $end_alloy-function

nextnano3 - Tutorial

next generation 3D nano device simulator

1D Tutorial - Part 6

Piezoelectric fields due to strain (Quantum well)

Piezoelectric fields

nextnano³ - Tutorial