nextnano³ - Tutorial

next generation 3D nano device simulator

3D Tutorial

Cleaved edge overgrowth quantum dots (CEO QDs)

Author: Stefan Birner

If you want to obtain the input files that are used within this tutorial, please check if you can find them in the installation directory.
If you cannot find them, please submit a Support Ticket.
 -> 3DTshapedQD_CEO_4nm_no_exciton.in - (The calculation takes 13 minutes SYSTEM time and 38 minutes CPU time on a modern Quad-core CPU.)
 -> 3DTshapedQD_CEO_4nm.in
 -> 3DTshapedQD_CEO_5nm.in
 -> 3DTshapedQD_CEO_7nm.in
 -> 3DTshapedQD_CEO_9nm.in
 

Cleaved edge overgrowth quantum dots (CEO QDs)

• This tutorial is based on the paper of
  
      M. Grundmann, D. Bimberg
      Formation of quantum dots in twofold cleaved edge overgrowth
      Phys. Rev. B 55 (7), 4054 (1997).
  
  The purpose is to benchmark the nextnano³ code to their numerical calculations.
   
• We study T-shaped cleaved edge overgrowth quantum dots (CEO QDs) that consist of three perpendicularly oriented quantum wells that are placed inside a 65 nm x 65 nm x 65 nm cuboid of Al_0.35Ga_0.65As.
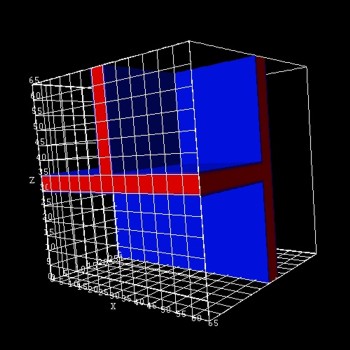
  If the width of all three GaAs quantum wells is 5 nm, the structure looks as follows:

• The axes are oriented the following way:
  
    $domain-coordinates
   ...
   hkl-x-direction-zb = 0  0  1  ! along the [001]  direction in the crystal coordinate system (1^st  growth direction, i.e. 1^st  QW)
   hkl-y-direction-zb = 1 -1  0  ! along the [1-10] direction in the crystal coordinate system (3^rd  growth direction, i.e. 3^rd QW)
  !hkl-z-direction-zb = 1  1  0  ! along the [110]  direction in the crystal coordinate system (2^nd growth direction, i.e. 2^nd QW)
 
• The intersection of the three T-shaped quantum wires (QWRs) forms the quantum dot (i.e. in the middle of the structure).
   
• In accordance to the above cited paper, we solve the single-band Schrödinger equation using isotropic effective masses for the electrons and for the heavy holes.
  We use Neumann boundary conditions for the Schrödinger equation.
  
  The Schrödinger matrix has dimension N = N_x * N_y * N_z = 65 * 65 * 65 = 274625.
  (65 grid points in each direction, i.e. a 1 nm grid spacing.)
   
• From the calculated single-particle electron and heavy hole ground states, we calculate the exciton binding energy within the Hartree approximation (Coulomb interaction).
  The algorithm is as follows:
  
  1) Solve Schrödinger equation for the single-particle energies and wave functions  of the electron     (empty dot).
  2) Solve Schrödinger equation for the single-particle energies and wave functions  of the heavy hole (empty dot).
  
  a) Solve Poisson equation for the electrostatic potential of the electron     ground state density.
  b) Solve Schrödinger equation for the single-particle energies and wave functions  of the heavy hole including electrostatic potential of electron.
  c) Solve Poisson equation for the electrostatic potential of the heavy hole ground state density.
  d) Solve Schrödinger equation for the single-particle energies and wave functions  of the electron     including electrostatic potential of electron.
  
  Iterate a), b), c), d) until convergence of exciton energy. (It usually converges within 4-5 iterations.)
  
  The total number of iterations and the residual can be specified in the input file:
  
    $numeric-control
   ...
   coulomb-matrix-element                = yes
   calculate-exciton                     = yes
   exciton-iterations                    = 7     ! number of iterations for exciton convergence
   exciton-residual                      = 1d-5  ! residual for exciton convergence criteria
   exciton-electron-state-number         = 1     ! 1 = electron ground state
   exciton-hole-state-number             = 1     ! 1 = hole      ground state
   number-of-electron-states-for-exciton = 1     ! 1 = only one electron state to be considered
   number-of-hole-states-for-exciton     = 1     ! 1 = only one hole      state to be considered
   
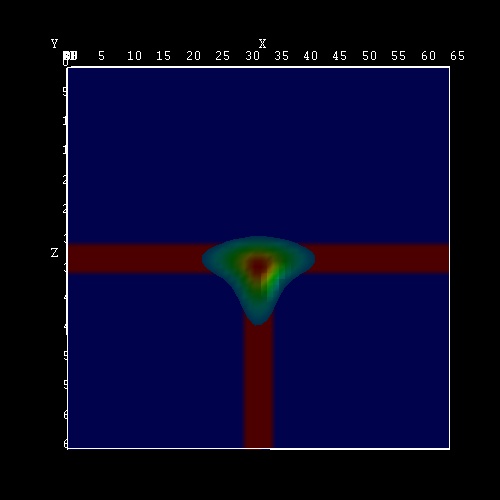
• The following figure shows the square of the (excitonic) electron wave function (70 % of psi²).
  
  
   
• The following figure shows the square of the (excitonic) electron wave function (slice inside the third quantum well plane, i.e. the slice is only through GaAs).
  Note that the slice of the material grid is below the third quantum well plane (slice through Al_0.35Ga_0.65As/GaAs).
  
  The x axis is along the [001] direction in the crystal coordinate system (1^st  growth direction, i.e. 1^st  QW).
The z axis is along the [110] direction in the crystal coordinate system (2^nd growth direction, i.e. 2^nd QW).
The plane that is shown is the (1-10) plane.

  
   
• The calculated exciton binding energies for CEO QDs of lengths 4 nm, 5 nm,  7 nm and 9 nm are shown in the following figure.
  
  
  
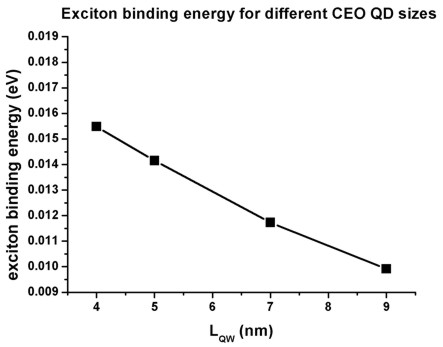
  The results are in reasonable agreement with Grundmann's paper although our values are about 2 meV smaller.
  We solved the Schrödinger and Poisson equations on a homogenous 65 nm x 65 nm x 65 nm grid using a grid resolution of 1 nm (which is a rather coarse grid), i.e. the total number of grid points is 66 x 66 x 66 = 287496.